The Skyline Problem

This page explains Java solution to problem The Skyline Problem using TreeMap data structure.

Problem Statement

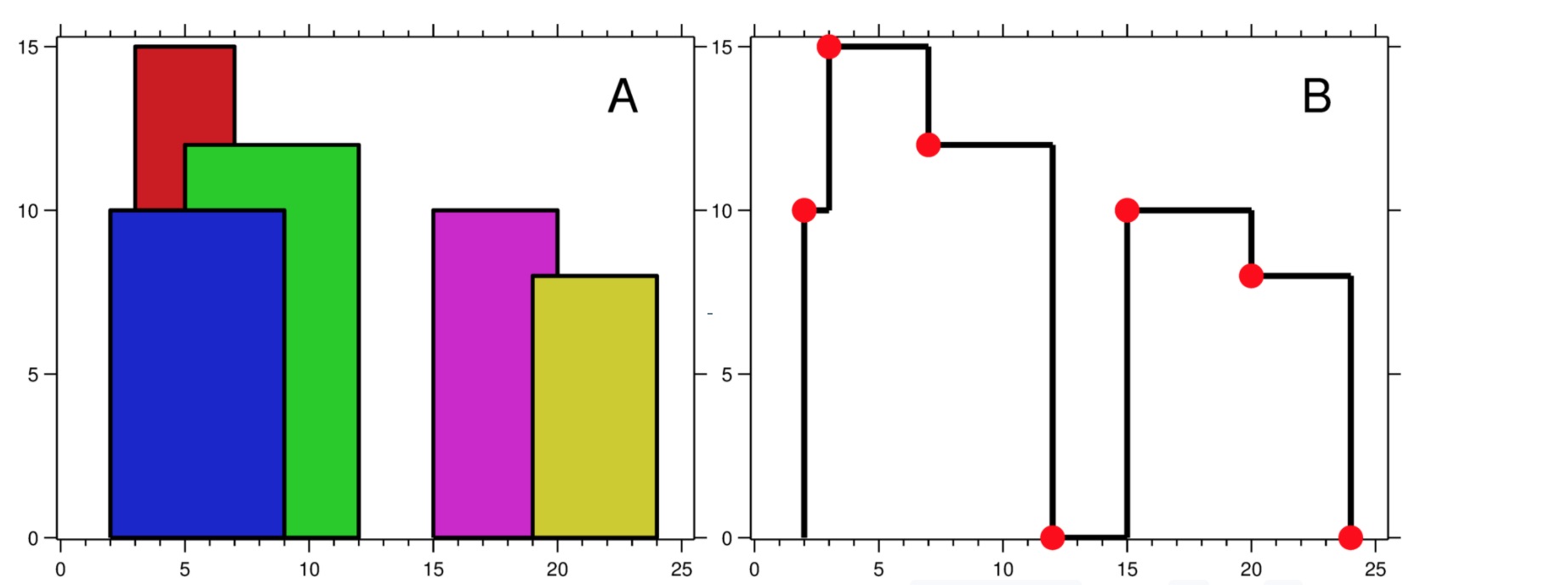
A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to output the skyline formed by these buildings collectively (Figure B).

The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

For instance, the dimensions of all buildings in Figure A are recorded as: [[2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8]].

The output is a list of "key points" (red dots in Figure B) in the format of [ [x1,y1], [x2, y2], [x3, y3], ... ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.

For instance, the skyline in Figure B should be represented as:[[2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0]].

Solution

package com.vc.hard;

import java.util.*;

class TheSkylineProblem {
    static class Interval {
        int x = 0;
        int y = 0;
        boolean isStart = false;

        Interval(int x, int y, boolean isStart) {
            this.x = x;
            this.y = y;
            this.isStart = isStart;
        }

        @Override
        public String toString() {
            return x+" "+y+" "+isStart;
        }
    }

    public List<List<Integer>> getSkyline(int[][] buildings) {
        //Response
        List<List<Integer>> res = new ArrayList<>();

        //Interval list
        List<Interval> list = new ArrayList<>();

        //Convert building array input into interval
        for(int[] building: buildings) {
            int start = building[0];
            int end = building[1];
            int height = building[2];
            list.add(new Interval(start, height, true));
            list.add(new Interval(end, height, false));
        }

        //Sort Interval list
        Collections.sort(list, new Comparator<Interval>(){
            public int compare(Interval i1, Interval i2) {
                int cmp = Integer.compare(i1.x, i2.x);
                if(cmp == 0) {
                    if(i1.isStart && i2.isStart) return Integer.compare(i2.y, i1.y);
                    else if(i1.isStart) return -1;
                    else if(i1.isStart) return 1;
                    else return Integer.compare(i1.y, i2.y);
                }
                return cmp;
            }
        });

        //Iterate over sorted interval list and update maxHeight based on interval
        TreeMap<Integer, Integer> map = new TreeMap<>();
        int prevMaxHeight = 0;
        int currentMaxHeight = 0;
        map.put(0, 1);
        for(Interval interval: list) {
            //If this is start add height of this building into the map
            if(interval.isStart) {
                map.put(interval.y, map.getOrDefault(interval.y, 0) + 1);
            }
            //Else remove height of this building from the map
            else {
                map.put(interval.y, map.getOrDefault(interval.y, 0) - 1);
                if(map.get(interval.y) == 0) map.remove(interval.y);
            }

            //See if maxHeight changes, if yes add the current interval to the result set
            currentMaxHeight = map.lastKey();
            if(currentMaxHeight != prevMaxHeight) {
                res.add(Arrays.asList(interval.x, currentMaxHeight));
                prevMaxHeight = currentMaxHeight;
            }
        }

        return res;
    }
}

Time Complexity

O(N log N) Where
N is total number of buildings in an input array

Space Complexity

O(N) Where
N is total number of buildings in an input array